Mål
Studenten skall efter avslutat laboration…
- …komma igång med laborationsmiljö och verktyg
- …förstå skillnaden mellan logiska (modell) och visuella(view) koordinatsystem.
- …skapat en applikation med funktionalitet som exempelapplikationen
Teori
Spel produceras för en rad plattformar med olika förutsättningar och upplösningar. Eftersom storleken på den visuella representationen av spelet kan variera, kan vi inte använda visuella “skärmkoordinater” för att hantera logiken i spelet.
Exempel:
Tänk spelet schack, en schackpjäs logiska position anges i logiska koordinater x=[0,7] y = [0,7]. Den logiska positionen används när vi implementerar reglerna, en AI-spelare och när vi sparar ett spel. En schackpjäs visuella representation bestäms utav en mängd faktorer:
- Skall spelet visas i 2D eller 3D?
- Upplösning på skärmen och fönstret som spelet visas i
- Storlek på bildrepresentationen av spelpjäserna, ex 128 * 128 pixlar
- Skall vi se hela brädet?, scrolla(2D)? styra en kamera(3D)?
- Skall spelet roteras, så att egen spelares pjäser finns längst ner?
För att rendera en sprite i monogame till skärmen kan vi till exempel använda SpriteBatch.Draw(Texture2D texture, Rectangle destinationRectangle, Color color) där destinationRectangle är koordinaterna i skärmkoordinater för platsen där vi ritar vår sprite.
Så för att omvandla från logiska spelkoordinater till skärmkoordinater behöver vi skriva en funktion som omvandlar mellan de två koordinatsystemen en “transformation”. I 3D-visualisering använder vi flera transformationer men det är lite utanför denna kurs där vi koncentrerar oss på 2D-representationer.
En schackpjäs står på plats x=3, y=2 på ett schackbräde x=[0,7] y = [0,7] där 0,0 är platsen för svart spelares högra(ur egen synvinkel) torn (a8) och 7,7 är koordinaten för vits högra(ur egen synvinkel) torn(h1). Vi ska räkna ut skärmkoordinater för pjäsens textur som är 64*64 texlar stor. Vi vill ha en kant som är 64 pixlar bred runt hela spelplanen för att få plats med lite text och ikoner. Hela spelplanen med kant blir då 64 + 8*64 + 64 pixlar bred.
För enkelhets skull spelar vi som vit och ritar då ut spelpjäsens övre vänstra hörn enligt följande:
int sizeOfTile = 64; int borderSize = 64; int visualX = borderSize + piece.x * sizeOfTile; int visualY = borderSize + piece.y * sizeOfTile;
Detta resulterar i att pjäsen på 3,2 får sitt övre vänstra hörn på de visuella koordinaterna (64+3*64), (64+2*64)
Uppgift 1. Kod

Skapa en klass “Camera” och i den skriv en metod som tar logiska koordinater och returnerar visuella koordinater enligt ovanstående exempel.
Testfall:
| Logisk koordinat | Visuell koordinat |
|---|---|
| 0,0 | 64, 64 |
| 7,0 | 512, 64 |
| 1,7 | 128, 512 |
| 7,7 | 512, 512 |
Uppgift 2. Rotation

Om vi nu istället spelar som svart vill vi rotera brädet i både x och y-led för att svart spelares pjäser skall renderas i underkant.
Fyll i följande tabell.
| Logisk koordinat | Visuell koordinat |
|---|---|
| 0,0 | |
| 6,0 | |
| 2,7 | |
| 7,7 |
Skriv ännu en metod i Camera klassen som räknar ut de visuella koordinaterna för en spelpjäs på där spelbrädet är roterat för att ses ur svart spelares synvinkel.
Uppgift 3. Skalning


Vi har nu en plattform där skärmen är mindre än 640 * 640 pixlar vill vi skala om spelet till att passa storleken 320 * 240.
Skriv en till metod i Camera klassen som ger de visuella koordinaterna för vit eller svart spelare där vi skalar ner spelet så att hela spelplanen syns på skärmen.
Uppgift 4.

Skriv ett program där en boll med diametern 0.1 studsar på insidorna av ett rum med storleken 1 * 1. Runt kanterna på “spelplanen” skall det finnas en kant så att man tydligt ser var bollen kan studsa. Programmet skall kunna anpassas till olika skärm-storlekar genom hårdkodning.
Animeringen skall ske i logiska(modell)-koordinater(0-1,0-1) och sedan transformeras till lämpliga fönsterkoordinater. Runt spelplanen skall en ram ritas ut som har samma storlek i pixlar oavsett fönsterupplösning.
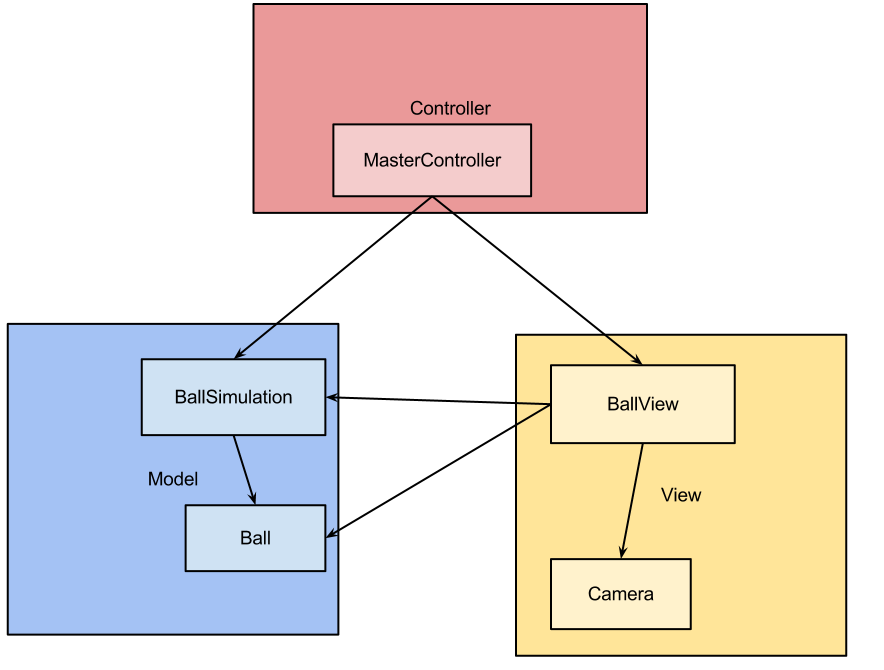
Dela upp koden i följande klasser:
- Ball: Innehåller bollens egenskaper. Position, Hastighet och radie.
- BallSimulation: Innehåller en instans av Ball och förflyttnings och kollisionskoden
- Camera: Översätter logiska koordinater till vy-koordinater
- BallView: Innehåller en instans av Camera och känner även till BallSimulation för att kunna rita ut bollen och spelarean
- MasterController: Ärver från Microsoft.Xna.Framework.Game. Innehåller instans av BallSimulation och BallView.